Non Linear FEA, Polymers, Thermoplastics

Non Linear FEA, Polymers, Thermoplastics

The field of non-linear analysis of plastics is one rife with challenges, not the least of which is getting accurate results. Unfortunately, the vast majority of analysis projects have results that are disappointing to practitioners and technical directors alike.

“Why analysis of plastic parts so often wrong”

Innova has spent many years refining analysis techniques to provide fast and accurate solutions for complex non-linear problems.

Despite the challenges, there are some tricks to achieve good results. This section of the website will provide a brief overview of some of these techniques.

Reasons to use non linear analysis in plastic part design

Linear analysis of plastics often provides poor results when used for in typical injection molded part design. Even parts that do not yield are often poorly represented by linear analysis tools.

Non linear solvers and advanced analysis techniques can offer many benefits:

  • Accurate representation of structural properties of injection molded plastics.
  • Study of part design accommodating environmental variables such as temperature, speed of loading, and time dependencies.
  • Creep studies for fast, accurate results of long term aging.
  • Drop test simulation.
  • Incorporation of dimensional variation on part performances.
  • Importation of molding stresses as an initial condition.

Most plastic part designers insist on a full non linear characterization of the structural behavior of a proposed design before tooling release. This can eliminate many field failures, unanticipated part performance, and full understanding of part functionality at all ranges of manufacturing tolerances.

Listed below are some technical details as to how these tools can be best utilized for robust analysis of thermoplastics.

Material properties

The first step in any meaningful non-linear analysis of plastics is to obtain accurate stress/strain curves for type of loading anticipated in the analysis. For example, if a compression load is anticipated from a given part, obtaining tension data may not be the best approach for good results, even though tension data is usually more readily available than compression. Unlike metals, many polymers have dramatically different material properties depending on the direction, type, and speed of the load application.
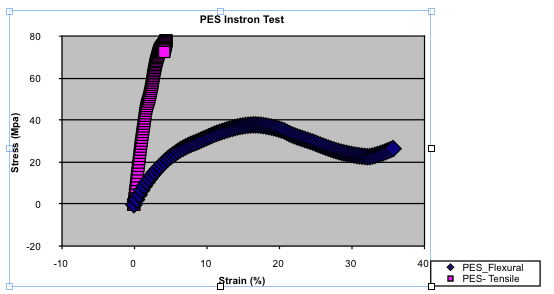
Figure 1.) PES Instron Test

Figure 1.) PES Instron Test

Figure 1 above shows the same thermoplastic undergoing different Instron tests. It can be seen that using the readily available tensile data for a part that sees flexural loading will provide unsatisfactory solutions- the data is completely different.

This is typical of many thermoplastics, and it is imperative that the correct material properties be obtained for each job.

Another consideration for testing materials is to remember that most polymers are strain rate dependent meaning that the speed at which the test is administered should match the speed at which the load is applied as closely as possible. Many thermoplastics are capable of absorbing short duration impact loads at a much higher rate than if the load is applied slowly. It is important to map the test speed to the actual way the part is loaded during service.

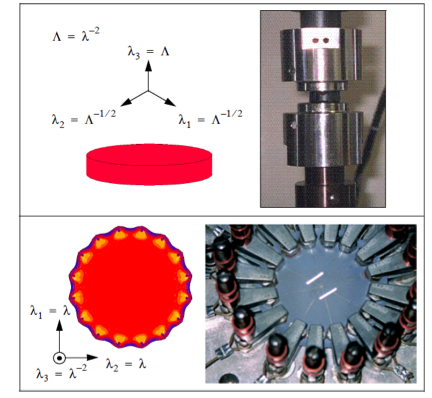
Figure 2.) Bi-axial strain test

Figure 2.) Bi-axial strain test

Figure 2 shows a unique means of testing a material sample to obtain both tensile and compressive properties in a single test.

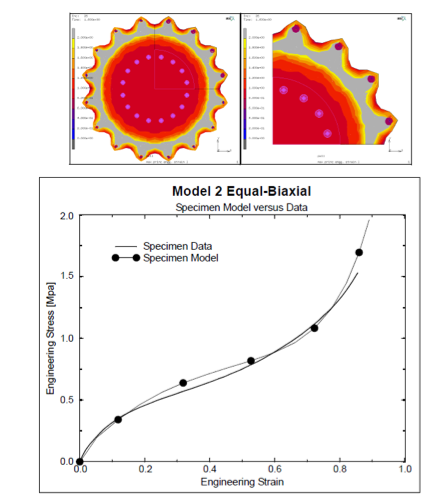
Figure 3.) Validating materials data-predicted vs. actual

Figure 3.) Validating materials data-predicted vs. actual

An important step in FEA is validation hat the material model correlates well tot eh test coupon. Once properties are recovered from the test sample, an FEA model of the coupon can be created in the simulation environment, and the results should correlate well to the physical test.

If the correlation is accurate, confidence is gained that the actual part geometry will also correlate well.

Meshing

Creating a robust and accurate mesh is another key to good solutions. Innova uses automated global and localize remeshing strategies extensively to manage tricky non-linear problems, these pictures show some simplistic examples of typical meshing strategies.
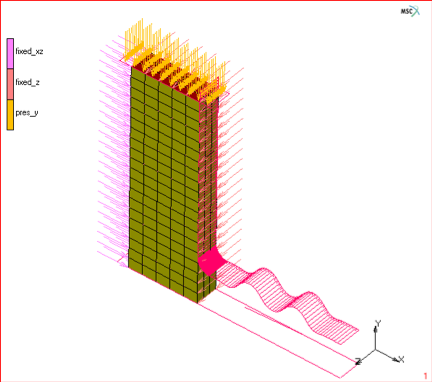
Figure 4.) 3D global remeshing of an elastomer.

Figure 4.) 3D global remeshing of an elastomer.

Figure 5.) 3D global remeshing of an elastomer.

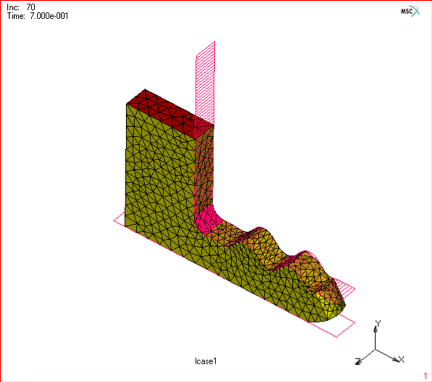
Figure 5.) 3D global remeshing of an elastomer.


Figure 6.) 3D global remeshing of an contact problem.

Figure 6.) 3D global remeshing of an contact problem.

Challenging Problems

With accurate material properties and a good, effective meshing strategy, we can take on challenging problems with full confidence that our solutions will be relevant.

Some examples of nonlinear analysis problems are presented:

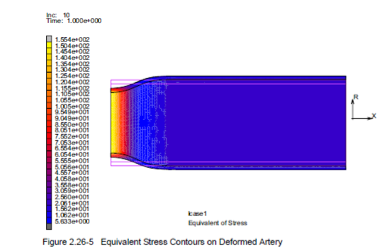
Figure 7.) Fluid structure interaction of arterial stress.

Figure 7.) Fluid structure interaction of arterial stress.

Figure 8.) Large deformation of elastomeric part

Figure 8.) Large deformation of elastomeric part


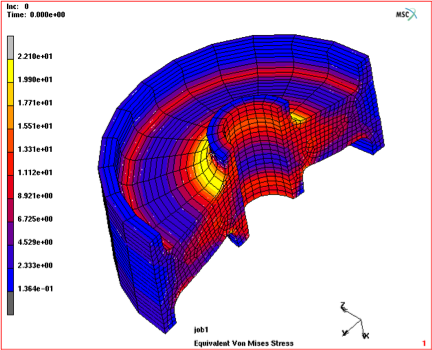
Figure 9.) Wall thickness optimization

Figure 9.) Wall thickness optimization

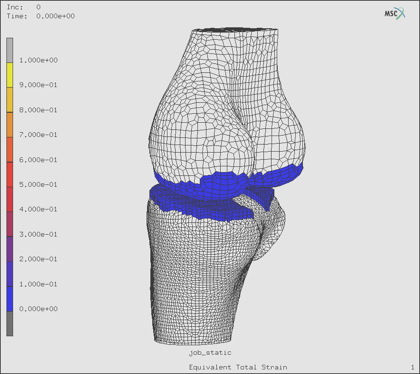
Figure 10.) Complex anatomical meshing

Figure 10.) Complex anatomical meshing

Structural Analysis-Explicit

Often, high speed impact events must be simulated, this can include manufacturing operations, drop testing, and devices that undergo high speed events.

Figure 11.) Dynamic impact-forming

Contact Innova for materials testing, and non linear analysis of thermoplastic part behavior

Recent Work